2019-12-24 click: 5074
摘要：圓弧圓柱蝸桿傳動在工業自動化發展中具有重要地位，為確保使用過程中的穩定性和可靠性，必須對蝸桿的精度進行檢測和分析，所以對圓弧圓柱蝸桿的各項誤差測量也是目前行業研究的重點與難點。根據國標要求，圓弧圓柱蝸桿測量項目主要包括齒廓、螺旋線和齒距三項，其中螺旋線與齒距測量相對簡單。本文重點討論圓弧圓柱蝸桿軸截面齒廓的測量，基于圓弧圓柱蝸桿軸截面齒廓成型原理，建立蝸桿軸截面齒廓方程，在CNC齒輪測量中心上采用樣條插補運動實現對圓弧圓柱蝸桿軸截面齒廓的測量，并對其采集誤差數據進行分離與補償，成功實現了對圓弧圓柱蝸桿軸截面齒廓的測量，進一步提高了測量結果的準確度和精度。
關鍵字：圓弧圓柱蝸桿；CNC齒輪測量中心；齒廓測量；
0．引言
圓弧圓柱蝸桿是一種非直紋面圓柱蝸桿，其齒面一般為圓弧形凹面。按照加工原理不同可分為圓環面包絡圓柱蝸桿（ZC1）、圓環面圓柱蝸桿（ZC2）和軸向圓弧齒圓柱蝸桿（ZC3）三種類型[1]。經過理論分析，實驗研究以及在工業上的使用證明，在相同條件下，與普通圓柱蝸桿相比，圓弧圓柱蝸桿具有承載能力大，嚙合性能好，接觸面積大，傳動效率高，結構緊湊，使用壽命長等優點，廣泛應用于冶金、機械和化工等行業的重載設備中，這種以線共扼為嚙合特征的蝸桿傳動對制造和安裝誤差及熱處理變形等較為敏感，由于誤差的影響，齒面容易發生邊緣接觸，常常導致蝸輪副的早期損傷和實效破壞[2]。因而對圓弧圓柱蝸桿的齒廓測量至關重要，要求在加工過程中對誤差進行控制，嚴格控制圓弧圓柱蝸桿的齒廓誤差，提高圓弧圓柱蝸桿的制造精度。
圓弧圓柱蝸桿測量是目前行業面臨的一個新的技術問題。圓弧圓柱蝸桿測量主要包括齒廓，螺旋線以及齒距三個測量項目，一般螺旋線與齒距的測量相對簡單容易，針對齒廓測量，由于圓弧圓柱蝸桿加工原理的不同，其蝸桿軸截面齒廓曲線也不同，既而蝸桿的軸截面齒廓表達式也不同，較為復雜。為解決圓弧圓柱蝸桿的齒廓測量，哈爾濱精達測量儀器有限公司與北京工業大學精密工程研究所合作，共同研究圓弧圓柱蝸桿的軸截面齒廓成型原理，建立圓弧圓柱蝸桿軸截面齒廓測量的數學模型，進一步實現圓弧圓柱蝸桿軸截面齒廓測量，由于圓弧圓柱蝸桿軸截面齒廓為圓弧形凹廓，所以在測量過程中測球與齒廓接觸點的法矢不斷變化，存在測頭半徑補償問題。本文提出一種基于CNC齒輪測量中心圓弧圓柱蝸桿軸截面齒廓的測量方案，并重點討論相應誤差處理方法及測頭補償方法。
1．圓弧圓柱蝸桿軸截面齒廓方程建立
1.1圓環面包絡圓柱蝸桿（ZC1）
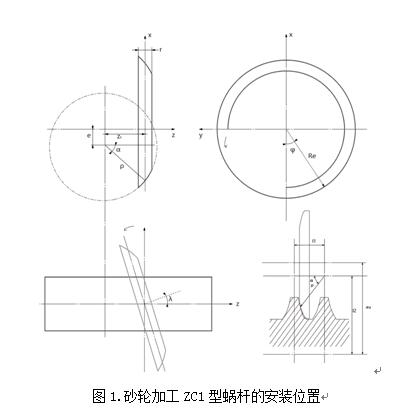
圓環面包絡圓柱蝸桿齒面是由圓環面（軸截面為圓弧的砂輪）包絡形成的，磨削時，蝸桿軸線與砂輪軸線的軸交角等于蝸桿分度圓柱導程角，該兩軸線的公垂線通過蝸桿某一位置（依實際情況，單面砂輪為齒廓分度圓處，雙面砂輪為蝸桿齒槽中點）[3~4]，砂輪表面與蝸桿齒面的瞬時接觸線是一條固定的空間曲線，由齒廓形成原理可知（如圖1所示），經過建立坐標方程推導出軸截面齒廓方程為：
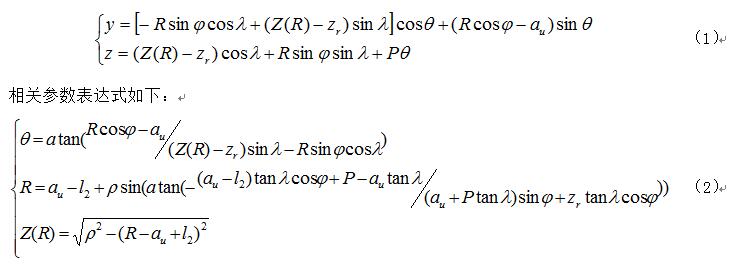
由表達式（2）可計算出相應參數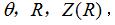 
，進一步代入表達式（1）中可求解圓環面包絡圓柱蝸桿（ZC1）的軸截面齒廓坐標。
式中：y,z為軸截面齒廓坐標；
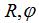分別為齒廓上點與加工砂輪接觸時，與加工砂輪軸線距離和回轉角；
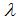為蝸桿導程角；
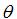為相對初始位置蝸桿轉角；
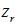為砂輪軸截面圓弧圓心到蝸桿與砂輪中垂線的距離，對于單面砂輪來說 
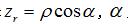,為砂輪分度圓點曲率半徑與砂輪軸線夾角，對于雙面砂輪來說， 
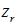由砂輪寬度計算，公垂線在齒槽中點；
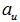為加工時砂輪軸線與蝸桿軸線最短距離；
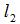為砂輪對蝸桿軸線偏轉之前砂輪軸截面圓心與蝸桿軸最短距離；
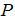為螺旋參數；
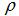為砂輪軸截面圓弧曲率半徑。
1.2圓環面圓柱蝸桿（ZC2）
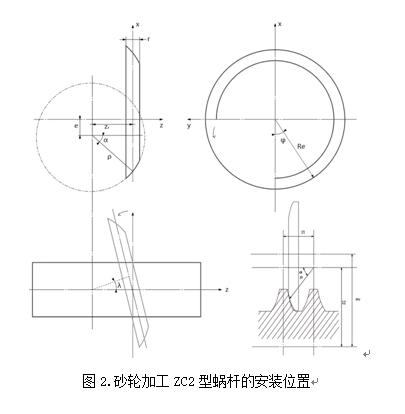
與圓環面包絡圓柱蝸桿（ZC1）都是磨削蝸桿，只是形成原理不同，安裝時，圓環面圓柱蝸桿（ZC2）是通過調整砂輪與蝸桿軸交錯角，使兩軸公垂線通過砂輪齒廓的曲率中心，這就意味著砂輪與蝸桿的瞬時接觸線變為與砂輪軸截面的圓弧重合的平面曲線。由齒廓形成原理可知（如圖2所示），經過建立坐標方程推導出軸截面齒廓方程為：
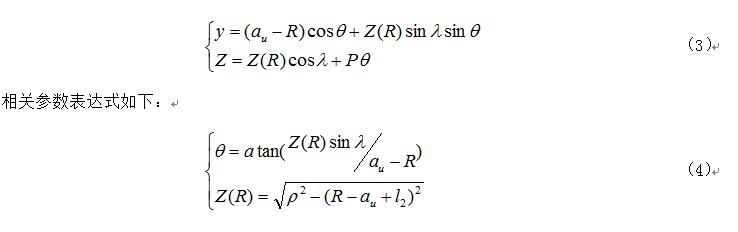
由表達式（4）可計算出相應參數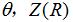 
，進一步代入表達式（3）中可求解圓環面圓柱蝸桿（ZC2）的軸截面齒廓坐標。
式中：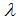 
為砂輪軸線與蝸桿軸線交錯角，由 
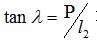求出；
其余參數意義同圓環面包絡圓柱蝸桿（ZC1）齒廓方程參數。
1.3軸向圓弧圓柱蝸桿（ZC3）
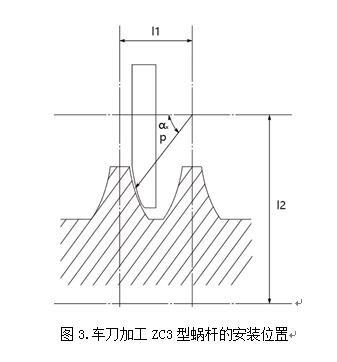
軸向圓弧圓柱蝸桿（ZC3）加工原理相對簡單，是由圓弧刃口的車刀車削而成，加工方式與阿基米德蝸桿類似，將車刀圓弧刃口置于蝸桿軸截面做相對螺旋運動，故軸向圓弧圓柱蝸桿（ZC3）軸截面齒廓為一段圓弧。由齒廓形成原理可知（如圖3所示），軸截面齒廓方程較為簡單，以y軸經過軸截面齒廓中點建立坐標方程推導出軸截面齒廓方程為：
2.圓弧圓柱蝸桿軸截面齒廓測量及誤差數據處理
2.1求解圓弧圓柱蝸桿軸截面齒廓坐標規劃測量軌跡
基于齒輪測量中心，求解圓弧圓柱蝸桿軸截面齒廓坐標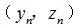 
，控制儀器Y軸和Z軸聯動實現蝸桿軸截面齒廓掃描測量，測頭的微變化量反映齒面加工誤差，如圖4所示。鑒于圓環面包絡圓柱蝸桿（ZC1）、圓環面圓柱蝸桿（ZC2）軸截面齒廓方程均為超越方程，其處理方式為根據變參數 
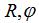離散得到一組足夠多的等間隔軸截面齒廓坐標點 
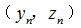，軸向圓弧圓柱蝸桿（ZC3）可通過軸截面齒廓方程直接獲取一組等間隔軸截面齒廓坐標點 
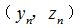。如果使用球形測頭對這三種蝸桿的軸截面齒廓進行測量，通過齒輪測量中心讀出的數據為測球中心的位置坐標，而不是測球球形表面和工件實際接觸點的位置坐標，這樣獲取的坐標值與理論接觸點坐標計算比較，得到的結果會有一定的誤差。為了便于測量和得到正確的測量結果，應對被測點進行測球半徑補償。因此需要將求解的蝸桿軸截面齒廓坐標點 
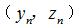轉換到與之對應的測球軌跡坐標點，這樣才能保證測球與工件接觸點與理論齒廓坐標點一致，避開了測球半徑導致接觸點變化給測量結果帶來的影響。即根據求解蝸桿軸截面齒廓坐標點 
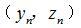，找到測球中心與對應接觸點的坐標之間的轉換關系，便可獲得測球測量軌跡的坐標。
問題的難點在于如何求取實際接觸點的法線方向，如果被測曲面的形狀已知，且可以用一定形式的解析函數表示，那么就可以用解析的方法求出曲面每個點的法線方向，按照求得的法線方向確定與理論齒廓相接觸的對應測球球心軌跡坐標，但是圓弧圓柱蝸桿的軸截面齒廓方程為超越方程，直接通過解析函數求出每個點的法線方向比較復雜。可以通過微平面法求解測球與工件接觸點的法矢，進一步求得與理論軸截面齒廓實際接觸點相對應的測球測量軌跡坐標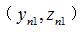 
由于這三種蝸桿軸截面齒廓均為復雜曲線，為實現實際測量軌跡接近理論曲線，通過上述軸截面齒廓方程離散獲得一組足夠多的等間隔采樣點，當離散點的最大間隔均低于測量精度的0.1倍時，就可認為離散出的點列等效于理論齒廓。本文采用GTS系列運動控制器中的PVT運動模式，該運動模式能實現單次走1024個點位且運動平滑。實際運動過程中依據采樣點位置選取包括采樣點在內的略小于1024個的點，實現采樣點位置的準確測量。
2.2誤差數據處理
在齒輪測量中心上對圓弧圓柱蝸桿進行測量時，把被測工件實際幾何形狀的坐標測量值與計算機所計算的理論坐標值進行比較，得到被測工件測量的實際偏差。由于在測量過程中，受到控制精度和外部環境的影響，實際Y軸和Z軸存在運動誤差，影響測量結果的精度，所以需要進行運動誤差補償。
（1）誤差數據的獲取
按照上述規劃測量路徑對其軸截面齒廓進行測量，測球與被測件實際接觸點就是理論齒廓坐標點，由于蝸桿存在加工誤差，在測量過程中，測頭在Z軸方向的變化量即為齒面加工誤差。實際被測點如果和理論坐標點完全重合，測頭變化量為零，即齒面誤差為零，但是由于齒面存在加工誤差，測頭會有微變化量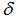 
，測球與工件實際接觸點假想在半徑無窮大的圓上，那么測頭的變化量 
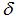等效于實際齒面加工誤差，對于測微小變化（10μm以內）該等效過程產生的偏差可忽略。
（2）運動誤差補償
無運動補償齒廓測量曲線波動較為明顯，這是因為在測量過程中受到運動誤差的影響，測頭微變化量并不能真實反映實際齒面誤差，所以需要進行運動誤差補償。即通過實時采集Y軸和Z軸數據，根據采集當前數據計算由于Y軸、Z軸運動誤差，帶來Z軸方向上的誤差分別為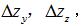 
，即蝸桿軸截面實際齒廓誤差 
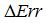為：
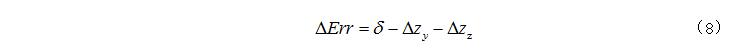
3.測量實驗
穩定性實驗是對同一ZC1型蝸桿的同一齒廓（以第一齒右齒面為例）進行多次（5次）測量，將結果進行比對。結果如表1。
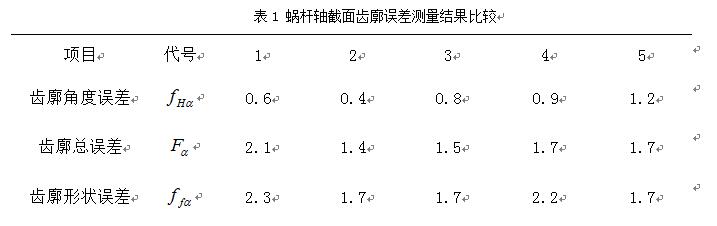
由表1中測量結果可以得出ZC1型蝸桿軸截面齒廓測量方法可行，同理可測ZC2型和ZC3型蝸桿，可以實現三種形式蝸桿軸截面齒廓的測量，并且測量結果穩定，精度和準確度很高。
4.總結
本文提出了一種圓弧圓柱蝸桿軸截面齒廓測量方法及誤差處理方法，成功實現了圓弧圓柱蝸桿軸截面齒廓的測量，并進一步提高了圓弧圓柱蝸桿軸截面齒廓測量的準確度和精度。通過測量結果對蝸桿軸截面齒廓誤差進行分析，并由此調整加工時蝸桿的安裝位置和加工圓弧圓柱蝸桿的加工參數，提高圓弧圓柱蝸桿的加工精度。經過實際測試表明，該測量方法正確可行，測量結果穩定、準確。
參考文獻：
[1]石照耀，葉勇，丁毅，張勇，姜志強.圓弧圓柱蝸桿的齒廓測量與參數反求[J].工具技術,1999(01):33-36.
[2]石萬凱，秦大同，田川寶.提高ZC1蝸桿制造精度的研究[J].重慶大學學報(自然科學版),1998(05):63-69.
[3]嚴以銳.圓弧齒圓柱蝸桿齒形的測量[J].機械工人.冷加工,1991(11):41-42.
[4]封增祺.圓弧圓柱蝸桿齒形計算[J].機械,1989(06):14-15.
